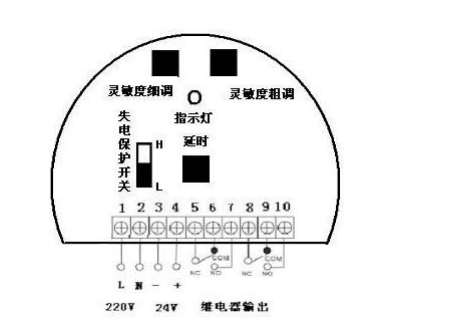
靈敏度是指儀表對被測參數變化的靈敏程度，或者說是對被測的量變化的反應能力，是在穩態下，輸出變化增量對輸入變化增量的比值：

靈敏度有時也稱“放大比”，也是儀表靜特性貼切線上各點的斜率。增加放大倍數可以提高儀表靈敏度，單純加大靈敏度并不改變儀表的基本性能，即儀表精度并沒有提高，相反有時會出現振蕩現象，造成輸出不穩定。儀表靈敏度應保持適當的量。

然而對于儀表用戶，諸如化工企業儀表工來講，儀表精度固然是一個重要指標，但在實際使用中，往往更強調儀表的穩定性和可靠性，因為化工企業檢測與過程控制儀表用于計量的為數不多，而大量的是用于檢測。另外，使用在過程控制系統中的檢測儀表其穩定性、可靠性比精度更為重要。

儀表精確度科稱精度，又稱準確度。精確度和誤差可以說是孿生兄弟，因為有誤差的存在，才有精確度這個概念。儀表精確度簡言之就是儀表測量值接近真值的準確程度，通常用相對百分誤差（也稱相對折合誤差）表示。

要提高儀表精確度，就要進行誤差分析。誤差通常可以分為疏忽誤差、緩變誤差、系統誤差和隨機誤差。疏忽誤差是指測量過程中人為造成的誤差，一則可以克服，二則和儀表本身沒有什么關系。緩變誤差是由于儀表內部元器件老化過程引起的，它可以用更換元器件、零部件或通過不斷校正加以克服和消除。系統誤差是指對同一被測參數進行多次重復測量時，所出現的數值大小或符號都相同的誤差，或按一定規律變化的誤差，可目前尚未被人們認識的偶然因素所引起，其數值大小和性質都不固定，難以估計，但可以通過統計方法從理論上估計其對檢測結果的影響。誤差來源主要指系統誤差和隨機誤差。在用誤差表示精度時，是指隨機誤差和系統誤差之和。

任何儀表都有一定的誤差。因此，使用儀表時必須先知道該儀表的精確程度，以便估計測量結果與約定真值的差距，即估計測量值的大小。儀表的精確度通常是用允許的最大引用誤差去掉百分號（%）后的數字來衡量的。

模擬式儀表的精確度一般不宜用絕對誤差（測量值與真實值的差）和相對誤差（絕對誤差與該點的真實值之比）來表示，因為前者不能體現對不同量程儀表的合理要求，后者很容易引起任何儀表都不能相信的誤解。例如，對一只滿量程為100mA的電流表，在測量零電流時，由于機械摩擦使表針的示數略偏離零位而得到0.2 mA的讀數，若按上述相對誤差的算法，那么該點的相對誤差即為無窮大，似乎這個儀表是完全不能使用的：但在工程人員看來，這樣的測量誤差是很容易理解的，根本不值得大驚小怪，它可能還是一只比較精密的儀表呢！ 模擬式儀表的合理精確度，應該以測量范圍中最大的絕對誤差和該儀表的測量范圍之比來衡量，這種比值稱為相對（于滿量程的）百分誤差。

按照儀表工業規定，儀表的精確度劃分成若干等級，簡稱精度等級，如0.1級、0.2級、0.5級、1.0級、1.5級、2.5級等。由此可見，精度等級的數字越小，精度越高。這就是儀表的靈敏度與精確度之間的關系。